Evrything You Need to Know About Cvp

Chapter xv – Toll-book Profit (CVP) Analysis and Break-Even Point

 – Introduction to CVP analysis

 – Calculations for a CVP analysis

 – Using a CVP to target a desired turn a profit

 – Pause-even point explained

 – Computing the break-even point

• Explicate how Toll-Book Turn a profit (CVP) analysis is related to planning for a profitable business
• Describe the relationship between sales volume, costs and profit
• Depict the notion of costs behavior (variable vs. fixed)
• List the assumptions behind a CVP analysis
• Calculate a CVP analysis using a pace-by-stride process
• Explicate the concept of a Break-Even Point
• Summate suspension-fifty-fifty points for both sales/acquirement dollars and number of units sold.

• CVP assay
• revenues and sales volume
• contribution margin income statement
• contribution margin
• contribution margin percentage
• variable costs/ expenses
• fixed costs/expenses
• operating income
• break-even point
• break-even sales
• break-fifty-fifty number of units sold

Introduction:

CVP analysis looks at the result of sales book variations on costs and operating profit. The analysis is based on the classification of expenses equally variable (expenses that vary in straight proportion to sales volume) or fixed (expenses that remain unchanged over the long term, irrespective of the sales volume). Accordingly, operating income is defined every bit follows:

Operating Income = Sales – Variable Costs – Fixed Costs

A CVP analysis is used to decide the sales volume required to achieve a specified profit level. Therefore, the analysis reveals the break-e ven betoken where the sales volume yields a net operating income of zero and the sales cutoff corporeality that generates the first dollar of turn a profit.

Toll-volume profit assay is an essential tool used to guide managerial, financial and investment decisions.

Cost-Volume Profit Analysis

Contribution Margin and Contribution Margin Percentage

The kickoff step required to perform a CVP analysis is to display the revenue and expense line items in a Contribution Margin Income Statement and compute the Contribution Margin Ratio.

A simplified Contribution Margin Income Statement classifies the line items and ratios as follows:

Contribution Margin Income Statement

Table xv.1 Contribution Margin Income Argument

Statement Particular	Amount	Percent of Income
Sales	$100	100%
(Deduction) Variable Costs	$lx	sixty%
(Full) Contribution Margin	$40	40% *
(Deduction) Fixed Costs	$xxx	30%
(Total) Operating Income	$10	10%

Table 15.1 Contribution Margin Income Statement.  The tabular array shows the pct of income for sales, contribution margin, and operating income are observed as totals, after variable and fixed cost deductions.

* Contribution Margin Percent

The method relies on the following assumptions:

• Sales price per unit is constant (i.e. each unit of measurement is sold at the same price);
• Variable costs per unit are constant (i.due east. each unit costs the same amount);
• Total fixed costs are constant (i.e. costs such as rent, property taxes or insurance exercise not vary with sales over the long term);
• Everything produced is sold;
• Costs are only affected because action changes.

The equation: Operating Income = Sales – Variable Costs – Fixed Costs

Sales = units sold Ten price per unit

Variable Costs = units sold 10 toll per unit

The first equation to a higher place tin can exist expanded to highlight the components of each line item:

Operating Income = (units sold X price per unit of measurement) – (units sold Ten cost per unit) – Fixed Cost

The contribution margin is defined equally Sales – Variable Costs. Therefore,

Contribution Margin ($) = (units sold X toll per unit) – (units sold X cost per unit)

And the Contribution Margin Percentage (CM%) is computed every bit follows:

CM% = Contribution Margin ($) / Sales ($)

Accordingly, the following is another way to express the relationship between contribution margin, CM percent, and sales:

Contribution Margin $ = Sales $ X Contribution Margin %

The contribution margin p ercentage indicates the portion each dollar of sales generates to pay for stock-still expenses (in our example, each dollar of sales generates $.forty that is bachelor to cover the stock-still costs).

As variable costs change in direct proportion (i.eastward. in %) of revenue, the contribution margin also changes in straight proportion to revenues, Nonetheless, the contribution margin per centum remains the aforementioned. Example:

Revenues  $100  – (xx units X $5)

Var. Costs $60 – lx% (20 units 10 60%)

CM              $xl    – 4 0%

The equation higher up demonstrates 100 percent of income ($100) minus $60 from variable costs equals $40 contribution margin. the equation below demonstrates revenues doubling to $200 and deducting stock-still costs of $120, that results in $80 contribution margin.

If revenues double :

Revenues      $200  – (xl units Ten $five)

Fixed Costs $120 –  60% (twoscore units X 60%)

CM                     $80       – 4 0%

Targeted Profit

CVP analysis is conducted to decide a acquirement level required to achieve a specified turn a profit. The acquirement may be expressed in number of units sold or in dollar amounts.

Income Statement

Table 15.2 Income Statement

Argument Item	Amount	Per centum of Income
Sales ( 20 units Ten $5)	$100	100%
(Deduction) Variable Costs (20 units Ten $three)	($threescore)	(60%)
(Total) Contribution Margin	$forty	40%
(Deduction) Fixed Costs	($30)	(thirty%)
(Full) Operating Income	$x	x%

Table 15.2 Income Argument. The table shows an income statement that observes total income from sales, contribution margin total afterward variable cost deduction, and operating income total afterwards fixed cost deduction.

How much sales is required to achieve a $20 turn a profit?
This tin be answered by finding the number of units sold or the sales dollar amount.

1. Required northward umber of u nits sold:

   Profit = Revenues – Variable Costs – Fixed Costs

   $20 = (Units Sold X $five) – (Units Sold 10 $iii) – $30
   $50 = (Units Sold X $5) – (Units Sold X $3)

   Sales deducted from Variable Costs is the definition of contribution margin

   $50 = (Units Sold) X ($5-$3)

   ($v-$3=$2 which is the $ contribution margin per unit of measurement)

   $fifty/$2 = 25 Units sold needed to achieve $20 in profit

   Units sold to achieve targeted profit = [latex]\huge{\frac{(\text{Fixed Costs Dollar + Targeted Profit Dollar})}{\text{Contribution Margin Dollar Per Unit}}}[/latex] The previous equation reads: units sold to achieve targeted profit, equals fixed costs dollars, plus targeted profit dollar, divided past contribution margin dollar per unit

   Verification:

   Income Statement

   Table 15.3 Income Argument

   Statement Item	Dollar Amount	Per centum of Income
   Sales (25 units X $5)	$1 25	100%
   (Deduction) Variable Costs (25 units X $3)	($75)	(60%)
   (Total) Contribution Margin (25 units Ten $2)	$ fifty	40%
   (Deduction) Fixed Costs	($30)	(30%)
   (Total) Targeted Operating Income	$ ii 0	x%

   Tabular array 15.three Income Statement.  The table shows an income statement that observes sales, contribution margin, and targeted operating income totals, afterwards variable and fixed cost deductions.

   Non due east : while O perating I ncome doubled, (from $ten to $xx) only 5 additional unit of measurement s sold (+25%) were required as only variable costs changed while fixed costs remained at $30 .

2. Required s ales dollar corporeality

   Turn a profit $ = sales $ – Variable Costs $ – Stock-still Costs $
   and
   Sales $ – Variable Costs $ = Contribution Margin $
   And then,
   Profit $ = Contribution Margin $ – Fixed Costs $

   Nosotros saw earlier that Contribution
   Margin $ can exist expressed every bit:
   Sales X Contribution Margin %

   Contribution Margin $ = (Sales $ x Contribution Margin %)

   Profit $ = (Sales $ x Contribution Margin%) – Stock-still Costs $

   Profit $ + Fixed Costs $ = (Sales $ x  Contribution Margin %)

   (Targeted Profit $ + Fixed Expense $) / Contribution Margin %  = Sales $

   The previous equation for Sales $ is calculated past calculation Targeted Turn a profit $ and Fixes Expense $, divided past Contribution Margin percentage

   Verification:

   Sales Required to attain $xx in targeted profit:

   ($20 + $xxx) / 40% = $125

   The case equation reads: $20 + $30, divided past xl percent equals $125

CVP formulas to be remembered:

• Required sales based on units sold to yield a targeted operating income:

Required number of units sold For Targeted Profit =

[latex]\huge{\frac{(\text{Fixed Costs Dollar + Targeted Profit Dollar})}{\text{Contribution Margin Dollar Per Unit}}}[/latex]

The previous equation reads: Required number of units sold for targeted turn a profit equals fixed costs dollar plus targeted profit dollar, divided by Contribution Margin dollar per unit.

• Required sales based on contribution margin percentage to yield a targeted operating income:

Required Dollar Sales For Targeted Profit =

 [latex]\huge{\frac{(\text{Fixed Costs Dollar + Targeted Profit Dollar})}{\text{Contribution Margin Percentage}}}[/latex]

The previos equation reads: Required dollar sales for targeted profit equals stock-still costs dollar plus targeted profit dollar, divided past Contribution Margin per centum.

Break-e ven Betoken

The interruption-even signal is reached when total costs and full revenues are equal, generating no proceeds or loss (Operating Income of $0). Business operators use the adding to determine how many product units they need to sell at a given price point to suspension even or to produce the first dollar of profit.

Break-even analysis is besides used in cost/profit analyses to verify how much incremental sales (or revenue) is needed to justify new investments.

The following graph illustrates the pause-even signal based on the number of covers sold in a restaurant

Figure 15.one Intermission-even point based on the number of covers sold in a restaurant

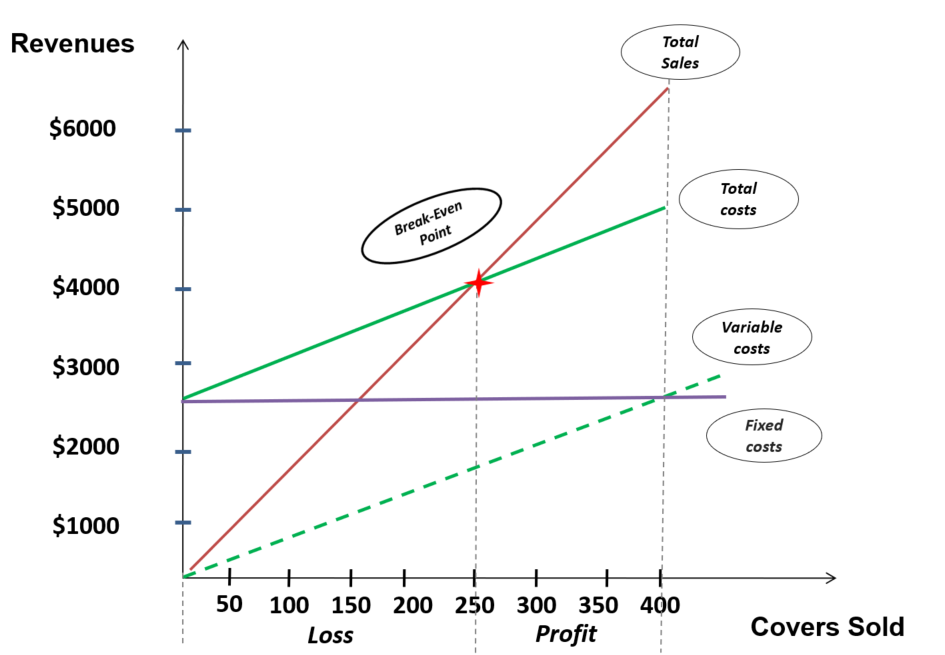
Long description:
A line graph with covers sold on the x axis. the x axis starts at 0, and has incriment markers in intervals of 50, increasing to a maximum of 400. At that place is a characterization for loss indicated from the start of the 10 axis ( 0 ) to the fifth interval marker ( 250 ). There is a characterization for profit indicated on the 10 centrality starting afterward the 250 marker. The Y centrality is labeled for revenues, as well starting at 0, incrementing by one thousand dollars every marker, to a maximum of vi thousand dollars. There are four lines graphed. 1 of which is a line representing total sales, which increases at linear rate, starting point (0 , $0), and ending point (400, $6000). Another line represents the full costs, which also increases at a linear rate. Its starting bespeak is (0 , $2500), and its ending point is (400, $5000). The total sales and total costs lines that are graphed, intersect at the point (250, $4000) which is labeled equally the interruption even betoken. the intersection of these two lines emphasize (equally the 10 axis turn a profit label does, which was mentioned earlier in this description) that profit occurs after 250 covers are sold. A fixed cost line is represented in this graph too.Starting indicate ( 0 , $2500), and ending point (400, $2500). Showing that fixed costs are static and not dependent on covers sold. The last line represents variable costs, starting point ( 0, $0) and ending point (400, $2500). Notice the catastrophe point of the total costs line equals the fixed cost and variable price totals.
End long clarification.

• The Sales line starts at the origin (0 revenue for 0 covers) and grows in direct proportion to the number of covers sold;
• Variable costs grow in straight proportion to Sales only at a slower rate. The line starts at the origin since no variable price arises if no auction occurs;
• The Fixed Costs line remains flat (unchanged irrespective of the number of covers sold). The operation incurs Stock-still Costs such equally rent whether the operation operates (is open for business) or not;
• Total Cost grows at the same rate every bit Variable Costs. The Total Cost minimum is represented past the Fixed Costs line;
• The Break-Even point occurs where the Total Sales line crosses the Total Costs line. In this illustration, the functioning starts being assisting when selling exceeds 250 covers.

Computing the Break-Fifty-fifty Point

Computing the break-fifty-fifty bespeak is equivalent to finding the sales that yield a targeted profit of zero.

Example

The average check (selling toll per encompass) for the Roadside Exotic BBQ Eatery is $16. The restaurant averages 85 covers sold a day or 2,250 covers per calendar month. The eatery currently loses money every bit indicated in the following statement:

Roadside Exotic BBQ Restaurant
Income Argument

Table 15.four Income Argument for an Exotic Barbecue Restaurant

Statement Item	Dollar Amount	Percent of Income
Sales ( 2,250 Covers x $ sixteen )	$ 40,800	100%
(Deduction) Variable Costs	($29,376)	(72%)
(Full) Contribution Margin	$11,424	28 %
(Deduction) Fixed Costs	($13,464)	(xxx%)
(Full) Operating Income	( $ 2,040)	(5 % )

Tabular array 15.four Income Statement for an Exotic Barbecue Restaurant.

The owner wants to know the sales volume required in terms of both dollars ($) and the number of covers for the restaurant to suspension even because its current expense structure.

1. Required number of covers sold

   Required number of covers sold =[latex]\huge{\frac{(\text{Fixed Costs Dollar + Targeted Profit Dollar})}{\text{Contribution Margin Dollar Per Unit of measurement}}}[/latex]

   The equation merely shown is meant to exist read equally: fixed costs dollar plus targeted profit dollar, divided by contribution margin dollar per unit

   In this case,

   • Targeted Turn a profit = cypher (definition of Break-even)
   • Contribution Margin per unit: $16 10 28% (CM%) = $four.48

   [latex]\huge{\frac{\text{Fixed Cost Dollar}}{\text{Contribution Margin Dollar /unit}} = \frac{\$ 13,464}{\$ 4.48}}[/latex] = three,005.36 (3,006) covers or

   100.18 (101) covers per day.

   Verification

   Roadside Exotic BBQ Restaurant
   Income Statement

   Tabular array 15.v Income Statement of an Exotic Barbecue Eatery

   Statement Particular	Dollar Ammount	Percent of Income
   Sales ( three, 00 5.36 Covers x $ 16 )	$48,0 8 6	100%
   (Deduction) Variable Costs	($34,622)	(72%)
   (Total) Contribution Margin	$13,46 4	28 %
   (Deduction) Stock-still Costs	($xiii,464)	(28%)
   (Full) Operating Income	($0)	( 0 % )

   Table 15.five Income Statement of an Exotic Barbecue Restaurant

2. Required Sales

   Sales $ = Targeted Turn a profit $ + Fixed Expense $
   Contribution Margin %

   Since targeted turn a profit is zero, the formula for the Break-Fifty-fifty Sales is:

   Fixed Expense $ = $13,464 = $48,086
   Contribution Margin % 28%

   Break-Even formulas to be remembered:

   • Break-Even number of Units sold

   Pause-Fifty-fifty number of units sold =

   (Fixed Costs Dolla r / Contribution Margin Dollar per unit)
   

   • Break-Even Sales

   Pause-Even Sales $ =

   (Fixed Costs Dollar / Contribution Margin Percentage)

Summary

The break-even indicate calculation allows nutrient service operators to calculate the number of covers (or units sold) or full sales needed to encompass all costs of the performance given the level of business generated. Once the intermission-even point is met, additional acquirement (or sales) starts to generate a profit, which is typically at least one purpose of running a business. Cost volume profit analysis allows the food service operator to summate similar figures just with a targeted turn a profit in mind. This CVP analysis is an essential tool in guiding managerial, financial and investment decisions for current operations or future business organisation ideas or plans.

Review Questions

Short Respond

1. How would conducting a cost volume profit analysis assistance a nutrient service operator make decisions about future business ideas?
2. What sort of assumptions need to exist fabricated about a food service operation in social club to complete a cost volume profit analysis
3. How might calculating a break-even point be useful to a food service manager?

Matching

Multiple Selection

Evrything You Need to Know About Cvp

Source: https://psu.pb.unizin.org/hmd329/chapter/cvp/

Share this post