Linear Inequalities and Systems of Linear Inequalities Review
nineteen.1: Review- Solve Linear Inequalities
- Page ID
- 46454
Past the stop of this section, you volition be able to:
- Graph inequalities on the number line
- Solve linear inequalities
- Translate words to an inequality and solve
- Solve applications with linear inequalities
Before you get started, take this readiness quiz.
- Interpret from algebra to English: \(xv>x\).
If you missed this problem, review [link]. - Interpret to an algebraic expression: \(15\) is less than \(x\).
If you missed this problem, review [link].
Graph Inequalities on the Number Line
What number would make the inequality \(10>3\) true? Are y'all thinking, "\(x\) could exist four"? That's correct, merely \(10\) could be half-dozen, too, or 37, or fifty-fifty 3.001. Any number greater than three is a solution to the inequality \(x>3\). We show all the solutions to the inequality \(x>three\) on the number line by shading in all the numbers to the right of 3, to testify that all numbers greater than three are solutions. Considering the number three itself is not a solution, we put an open parenthesis at three.
We can also stand for inequalities using interval note. There is no upper end to the solution to this inequality. In interval notation, nosotros express \(x>three\) as \((3,\infty)\). The symbol \(\infty\) is read as "infinity." It is not an actual number. Figure \(\PageIndex{1}\) shows both the number line and the interval note.
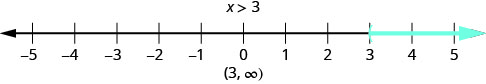
We use the left parenthesis symbol, (, to show that the endpoint of the inequality is not included. The left bracket symbol, [, shows that the endpoint is included.
The inequality \(x\leq one\) means all numbers less than or equal to 1. Hither nosotros need to show that ane is a solution, too. Nosotros exercise that by putting a subclass at \(x=1\). We then shade in all the numbers to the left of one, to evidence that all numbers less than one are solutions (Effigy \(\PageIndex{two}\)). At that place is no lower cease to those numbers. We write \(x\leq 1x\leq 1 \)in interval notation equally \((−\infty,1]\). The symbol \(−\infty\) is read every bit "negative infinity."
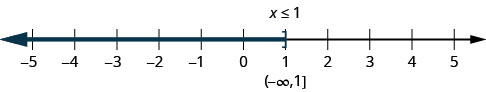
Effigy \(\PageIndex{3}\) shows both the number line and interval notation.

The annotation for inequalities on a number line and in interval notation use the same symbols to express the endpoints of intervals.
Graph each inequality on the number line and write in interval notation.
- \(x\geq −3\)
- \(x<2.five\)
- \(x\leq −\frac{3}{5}\)
- Reply
-
ⓐ
\( x \geq -3 \) Shade to the correct of \(−3\), and put a subclass at \(−3\). 
Write in interval notation. \( [-3, \infty) \) ⓑ
\( x < 2.5 \) Shade to the left of ii.five and put a parenthesis at ii.5. 
Write in interval notation. \( (-\infty, 2.5) \) ⓒ
\( ten \leq -\dfrac{3}{five} \) Shade to the left of \(−\frac{iii}{v}\), and put a subclass at \(−\frac{3}{5}\). 
Write in interval note. \( \bigg( -\infty, \dfrac{3}{5}\bigg] \)
Graph each inequality on the number line and write in interval notation:
- \(x>ii\)
- \(ten\leq −1.five\)
- \(x\geq \frac{three}{4}\).
- Respond
-
ⓐ
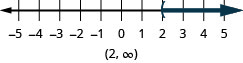
ⓑ
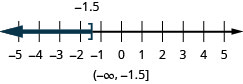
ⓒ
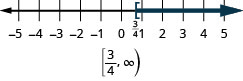
Graph each inequality on the number line and write in interval notation:
- \(10\leq −4\)
- \(x\geq 0.5\)
- \(x<−\frac{ii}{iii}\).
- Answer
-
ⓐ
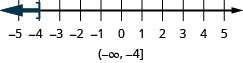
ⓑ

ⓒ
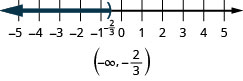
What numbers are greater than two just less than five? Are you thinking say, \(two.v,\infinite three,\space 3\frac{2}{3},\space 4,\space 4,\space 99\)? Nosotros tin can represent all the numbers between two and five with the inequality \(2<10<five\). Nosotros can bear witness \(2<x<five\) on the number line past shading all the numbers between 2 and 5. Again, we utilise the parentheses to show the numbers two and five are non included. Run into Figure.

Graph each inequality on the number line and write in interval annotation.
ⓐ \(−3<x<four\) ⓑ \(−half-dozen\leq x<−1\) ⓒ \(0\leq x\leq 2.5\)
- Respond
-
ⓐ
\(-3 < x < 4\) Shade between \(−3\) and four.
Put a parentheses at \(−3\) and 4.
Write in interval notation. \( (-3,four) \) ⓑ
\( -6 \leq x < -1 \) Shade between \(−6\) and −i.
Put a bracket at \(−vi\), and
a parenthesis at −i.
Write in interval notation. \( [-six,1) \) ⓒ
\( 0 \leq x \leq two.5 \) Shade between 0 and 2.5.
Put a bracket at 0 and at 2.v.
Write in interval notation. \( [0, 2.5] \)
Graph each inequality on the number line and write in interval notation:
ⓐ \(−2<x<1\) ⓑ \(−5\leq x<−four\) ⓒ \(1\leq x\leq 4.25\)
- Answer
-
ⓐ
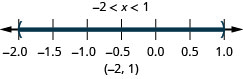
ⓑ
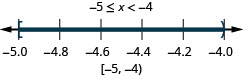
ⓒ
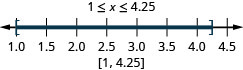
Graph each inequality on the number line and write in interval notation:
ⓐ \(−6<x<2\) ⓑ \(−3\leq ten< −ane\) ⓒ \(2.5\leq ten\leq 6\)
- Answer
-
ⓐ
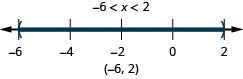
ⓑ
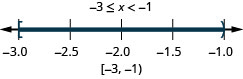
ⓒ
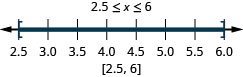
Solve Linear Inequalities
A linear inequality is much similar a linear equation—but the equal sign is replaced with an inequality sign. A linear inequality is an inequality in one variable that tin exist written in one of the forms, \(ax+b<c\), \(ax+b\leq c\), \(ax+b>c\), or \(ax+b\geq c\).
A linear inequality is an inequality in one variable that tin can be written in one of the post-obit forms where \(a, \, b,\) and \(c\) are real numbers and \(a≠0\):
\[ \begin{array} {llll} {ax+b<c,} &{ax+b\leq c,} &{ax+b>c,} &{ax+b\geq c.} \\ \nonumber \end{array}\]
When we solved linear equations, we were able to use the properties of equality to add, subtract, multiply, or divide both sides and still continue the equality. Like properties concur truthful for inequalities.
We can add together or subtract the same quantity from both sides of an inequality and yet keep the inequality. For example:
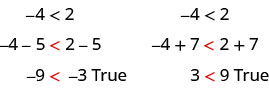
Detect that the inequality sign stayed the same.
This leads us to the Addition and Subtraction Properties of Inequality.
For any numbers \(a, \, b,\) and \(c,\) if \(a<b\), then
\[\begin{array} {ll} {a+c<b+c} &{a−c<b−c} \\ {a+c>b+c} &{a−c>b−c} \\ \nonumber \end{array}\]
We can add or subtract the same quantity from both sides of an inequality and still go along the inequality
What happens to an inequality when we divide or multiply both sides by a abiding?
Let's first multiply and split both sides by a positive number.
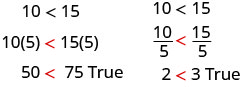
The inequality signs stayed the same.
Does the inequality stay the aforementioned when we divide or multiply by a negative number?
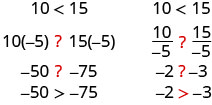
Notice that when we filled in the inequality signs, the inequality signs reversed their direction.
When we dissever or multiply an inequality by a positive number, the inequality sign stays the same. When we dissever or multiply an inequality by a negative number, the inequality sign reverses.
This gives u.s. the Multiplication and Division Property of Inequality.
For whatever numbers \(a, \, b,\) and \(c,\)
\[\begin{array} {50} {\text{multiply or divide by a positive}} \\ \\ \infinite\space\space\space\text{if }a<b\text{ and }c>0\text{, and so }ac<bc \text{ and }\frac{a}{c}<\frac{b}{c}. \\ \space\space\infinite\space\text{if }a>b\text{ and }c>0\text{, then }ac>bc \text{ and }\frac{a}{c}>\frac{b}{c}. \\ \\ \text{ multiply or dissever by a negative } \\ \\ \infinite\space\space\infinite\text{if }a<b\text{ and }c<0\text{, then }air-conditioning>bc \text{ and }\frac{a}{c}>\frac{b}{c}.\\ \space\infinite\space\space\text{if }a>b\text{ and }c<0\text{, then }ac<bc \text{ and }\frac{a}{c}<\frac{b}{c}.\\ \nonumber \end{assortment}\]
When we divide or multiply an inequality by \(a\):
- positive number, the inequality stays the same.
- negative number, the inequality reverses.
Sometimes when solving an inequality, as in the next case, the variable ends upon the right. We can rewrite the inequality in opposite to get the variable to the left.
\[ten>a \text{ has the same meaning as } a<10 \nonumber \]
Think about it as "If Xander is taller than Andy, then Andy is shorter than Xander."
Solve each inequality, graph the solution on the number line, and write the solution in interval notation:
ⓐ \(p−\frac{iii}{iv}\geq \frac{ane}{half dozen}\) ⓑ \(9c>72\) ⓒ \(24\leq \frac{three}{8}grand\)
- Answer
-
ⓐ
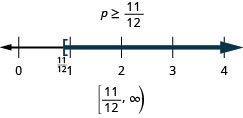
ⓑ
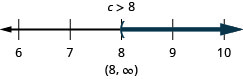
ⓒ
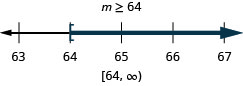
Solve each inequality, graph the solution on the number line, and write the solution in interval notation:
ⓐ \(r−\frac{1}{iii}\leq \frac{7}{12}\) ⓑ \(12d\leq 60\) ⓒ \(−24<\frac{4}{three}n\)
- Reply
-
ⓐ
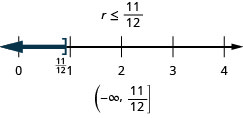
ⓑ
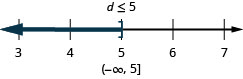
ⓒ
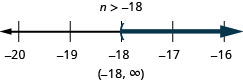
Be conscientious when you multiply or dissever by a negative number—recollect to reverse the inequality sign.
Solve each inequality, graph the solution on the number line, and write the solution in interval notation.
ⓐ \(−\frac{1}{3}m\geq \frac{6}{5}\) ⓑ \(\frac{n}{−ii} \geq 8\)
- Answer
-
ⓐ
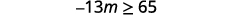
Divide both sides of the inequality by \(−\frac{1}{3}\).
Since \(−\frac{1}{3}\) is a negative, the inequality reverses.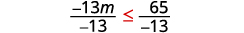
Simplify. 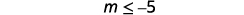
Graph the solution on the number line. 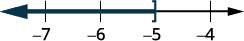
Write the solution in interval annotation. 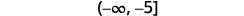
ⓑ
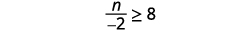
Multiply both sides of the inequality by \(−2\).
Since \(−2\) is a negative, the inequality reverses.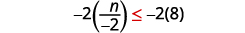
Simplify. 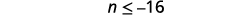
Graph the solution on the number line. 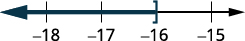
Write the solution in interval note. 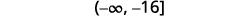
Solve each inequality, graph the solution on the number line, and write the solution in interval note:
ⓐ \(−8q<32\) ⓑ \(\frac{thou}{−12} \leq 15\).
- Respond
-
ⓐ
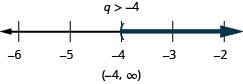
ⓑ
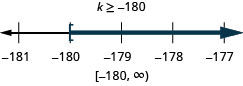
Solve each inequality, graph the solution on the number line, and write the solution in interval notation:
ⓐ \(−7r\leq −70\) ⓑ \(\frac{u}{−4}\geq −16\).
- Reply
-
ⓐ
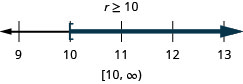
ⓑ
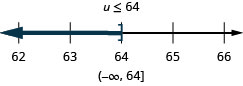
Most inequalities volition take more than than one step to solve. We follow the same steps we used in the general strategy for solving linear equations, simply make sure to pay close attention when we multiply or divide to isolate the variable.
Solve the inequality, graph the solution on the number line, and write the solution in interval notation: \(3q\geq 7q−23\).
- Respond
-
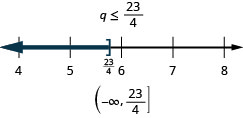
Solve the inequality, graph the solution on the number line, and write the solution in interval notation: \(6x<10x+19\).
- Answer
-
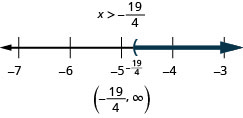
When solving inequalities, it is usually easiest to collect the variables on the side where the coefficient of the variable is largest. This eliminates negative coefficients and so we don't have to multiply or separate by a negative—which ways nosotros don't have to remember to reverse the inequality sign.
Solve the inequality \(8p+3(p−12)>7p−28\), graph the solution on the number line, and write the solution in interval note.
- Answer
-
\(8p+3(p−12)>7p−28\) Simplify each side as much equally possible. Distribute. \(8p+3p−36>7p−28\) Combine like terms. \(11p−36>7p−28\) Subtract \(7p\) from both sides to collect the
variables on the left, since \(xi>7\).\(11p−36−7p>7p−28−7p\) Simplify. \(4p−36>−28\) Add \(36\) to both sides to collect the
constants on the right.\(4p−36+36>−28+36\) Simplify. \(4p>eight\) Divide both sides of the inequality by
\(four\); the inequality stays the same.\(\dfrac{4p}{4}>\dfrac{eight}{4}\) Simplify. \(p>two\) Graph the solution on the number line. 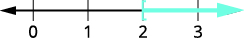
Write the solution in interval notation. \((2,\infty)\)
Solve the inequality \(9y+2(y+6)>5y−24\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
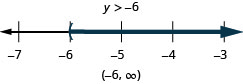
Solve the inequality \(6u+8(u−1)>10u+32\), graph the solution on the number line, and write the solution in interval note.
- Answer
-
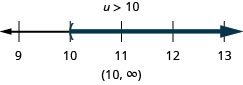
Just like some equations are identities and some are contradictions, inequalities may be identities or contradictions, besides. We recognize these forms when we are left with only constants as nosotros solve the inequality. If the upshot is a true statement, we have an identity. If the result is a fake argument, we take a contradiction.
Solve the inequality \(8x−two(5−x)<four(x+9)+6x\), graph the solution on the number line, and write the solution in interval annotation.
- Reply
-
Simplify each side every bit much as possible. \(8x−2(5−x)<4(x+9)+6x\) Distribute. \(8x−ten+2x<4x+36+6x\) Combine similar terms. \(10x−10<10x+36\) Subtract \({\color{cherry}{10x}}\) from both sides to collect the variables on the left. \(10x−x\,{\colour{red}{-\,10x}}<10x+36\,{\colour{red}{-\,10x}}\) Simplify. \(−10<36\) The \(10\)'s are gone, and we have a true
statement.The inequality is an identity.
The solution is all real numbers.Graph the solution on the number line. 
Write the solution in interval notation. \((−\infty,\infty)\)
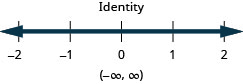
Solve the inequality \(4b−3(3−b)>5(b−half dozen)+2b\), graph the solution on the number line, and write the solution in interval notation.
- Respond
-
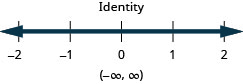
Solve the inequality \(9h−7(two−h)<8(h+xi)+8h\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
We tin can articulate fractions in inequalities much as we did in equations. Again, be conscientious with the signs when multiplying or dividing by a negative.
Solve the inequality \(\frac{1}{3}a−\frac{1}{8}a>\frac{five}{24}a+\frac{3}{iv}\), graph the solution on the number line, and write the solution in interval annotation.
- Answer
-
\(\frac{one}{3}a−\frac{1}{8}a>\frac{v}{24}a+\frac{3}{four}\) Multiply both sides past the LCD, 24,
to clear the fractions.\({\color{red}{24}}\left(\dfrac{1}{three}a−\dfrac{1}{8}a\right)>\,{\color{cherry-red}{24}}\left(\dfrac{5}{24}a+\dfrac{3}{4}\right)\) Simplify. \( 8a - 3a > 5a + 18 \) Combine similar terms. \( 5a > 5a + 18\) Decrease \(5a\) from both sides to collect the
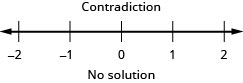
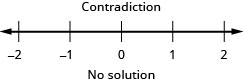
variables on the left.\( 5a \,{\color{red}{-\,5a}} > 5a \,{\color{red}{-\,5a}} + 18\) Simplify. \(0 > xviii \) The statement is false. The inequality is a contradiction.
There is no solution.Graph the solution on the number line. 
Write the solution in interval notation. There is no solution.
Solve the inequality \(\frac{one}{4}10−\frac{1}{12}x>\frac{1}{vi}10+\frac{seven}{8}\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
Solve the inequality \(\frac{ii}{v}z−\frac{i}{three}z<\frac{1}{xv}z−\frac{iii}{5}\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
Translate to an Inequality and Solve
To translate English sentences into inequalities, we need to recognize the phrases that point the inequality. Some words are easy, like "more than" and "less than." But others are not as obvious. Table shows some common phrases that point inequalities.
| \(>\) | \(\geq\) | \(<\) | \(\leq\) |
|---|---|---|---|
| \)" information-valign="heart" class="lt-math-17389">is greater than is more than is larger than exceeds | is greater than or equal to is at to the lowest degree is no less than is the minimum | is less than is smaller than has fewer than is lower than | is less than or equal to is at virtually is no more than is the maximum |
Translate and solve. And then graph the solution on the number line, and write the solution in interval notation.
\[\text{Twenty-seven less than }ten\text{ is at least }48.\nonumber\]
- Respond
-

Translate. \(x - 27 \geq 48\) Solve—add together 27 to both sides. \( ten - 27 \, {\colour{ruby}{+\, 27}} \geq 48 \, {\color{red}{+\, 27}}\) Simplify. \(x \geq 75\) Graph on the number line. 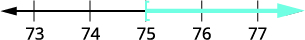
Write in interval notation. \([75, \infty)\)
Translate and solve. So graph the solution on the number line, and write the solution in interval note.
\[\text{Nineteen less than } p \text{ is no less than }47.\nonumber\]
- Respond
-
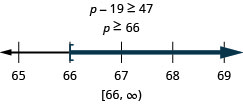
Interpret and solve. And so graph the solution on the number line, and write the solution in interval notation.
\[\text{Four more than }a\text{ is at virtually }fifteen.\nonumber\]
- Answer
-
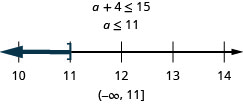
Solve Applications with Linear Inequalities
Many existent-life situations require us to solve inequalities. The method nosotros will use to solve applications with linear inequalities is very much like the one we used when we solved applications with equations.
Nosotros will read the problem and make certain all the words are understood. Side by side, we volition place what we are looking for and assign a variable to correspond it. Nosotros volition restate the problem in 1 sentence to brand it easy to translate into an inequality. Then, we volition solve the inequality.
Sometimes an application requires the solution to be a whole number, but the algebraic solution to the inequality is non a whole number. In that case, we must round the algebraic solution to a whole number. The context of the application will make up one's mind whether we circular upwards or down.
Dawn won a mini-grant of $iv,000 to buy tablet computers for her classroom. The tablets she would like to buy toll $254.12 each, including revenue enhancement and commitment. What is the maximum number of tablets Dawn can purchase?
- Answer
-
\(\begin{assortment} {ll} {\textbf{Step 1. Read }\text{ the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what y'all are looking for.}} &{\text{the maximum number of tablets Dawn can buy}} \\ {\textbf{Step 3. Name}\text{ what you are looking for.}} &{} \\ {} &{} \\ {} &{\text{Let }n= \text{ the number of tablets.}} \\ {\text{Cull a variable to represent that}} &{} \\{\text{quantity.}} &{} \\ {\textbf{Step 4. Translate.}\text{Write a sentence that gives the}} &{} \\ {\text{data to discover information technology.}} &{$254.12\text{ times the number of tablets is}} \\ {} &{\text{no more than }$iv,000.} \\ {} &{\space\space\space\space\space\space\space\space\infinite\space\infinite\space 254.12n\leq 4000} \\ {\text{Translate into an inequality.}} &{} \\ {\textbf{Step five. Solve }\text{the inequality.}} &{} \\ {} &{\space\infinite\space\space\infinite\space\space\space\space\space\space\space\infinite\infinite\space\space\space\space\space\space n\leq 15.74} \\ {} &{\space\infinite\space\space\space\space\space\space\space\space\space\space\space\infinite\infinite\space\space\infinite\space\space n\leq 15} \\{\text{But }n\text{ must exist a whole number of}} &{} \\ {\text{tablets, so round to }15.} &{} \\ {\textbf{Step 6. Bank check }\text{the reply in the trouble}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {} &{} \\ {} &{} \\ {\space\space\infinite \text{Rounding downwards the price to } $250, xv} &{} \\ {\infinite\space\space \text{tablets would cost }$3,750,\text{ while } 16} &{} \\ {\space\infinite\space \text{tablets would be }$4,000.\text{So a}} &{} \\ {\space\space\space \text{maximum of 15 tablets at }$254.12} &{} \\ {\space\space\space \text{seems reasonable.}} &{} \\ {\textbf{Step 7. Reply }\text{the question with a complete sentence.}} &{\text{Dawn tin can buy a maximum of 15 tablets.}} \\ \end{array}\)
Angie has $twenty to spend on juice boxes for her son'south preschool picnic. Each pack of juice boxes costs $2.63. What is the maximum number of packs she can buy?
- Answer
-
Angie can buy 7 packs of juice.
Daniel wants to surprise his girlfriend with a birthday party at her favorite restaurant. It will cost $42.75 per person for dinner, including tip and tax. His budget for the party is $500. What is the maximum number of people Daniel can take at the political party?
- Answer
-
Daniel tin can have xi people at the party.
Taleisha's phone programme costs her $28.80 a calendar month plus $0.20 per text message. How many text messages can she send/receive and keep her monthly phone bill no more $50?
- Answer
-
\(\brainstorm{array} {ll} {\textbf{Pace i. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the number of text messages Taleisha can brand}} \\ {\textbf{Footstep 3. Proper name }\text{what yous are looking for.}} &{} \\ {} &{} \\ {} &{\text{Let }t= \text{the number of text messages.}} \\ {\text{Choose a variable to stand for that}} &{} \\ {\text{quantity.}} &{} \\ {\textbf{Step iv. Translate }\text{Write a judgement that}} &{} \\ {\text{gives the information to notice information technology.}} &{$28.80\text{ plus }$0.20\text{ times the number of}} \\ {} &{\text{text messages is less than or equal to }$50.} \\ {} &{28.lxxx+0.20t \leq 50} \\ {\space\space\space \text{Translate into an inequality.}} &{} \\ {\textbf{Pace 5. Solve }\text{the inequality.}} &{} \\ {} &{\space\space\infinite\space\space\space\space\infinite\space\space\infinite\space\space\space\space 0.2t\leq 21.ii} \\ {} &{\space\infinite\space\space\space\space\infinite\space\infinite\space\infinite\infinite\space\space\space\space\space\infinite\infinite\infinite t\leq 106\text{ text messages}} \\ {} &{} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure information technology makes sense.}} &{} \\ {} &{} \\ {} &{} \\{\space\infinite\space \text{Yes, }28.80+0.20(106)=50.} &{} \\ {\textbf{Step seven. Write }\text{a sentence that answers the question.}} &{} \\ {} &{\text{Taleisha can send/receive no more than}} \\ {} &{106\text{ text letters to keep her bill no}} \\ {} &{\text{more than } $50.} \\ \end{array}\)
Sergio and Lizeth have a very tight holiday upkeep. They plan to rent a car from a visitor that charges $75 a week plus $0.25 a mile. How many miles tin they travel during the calendar week and notwithstanding proceed within their $200 budget?
- Respond
-
Sergio and Lizeth tin can travel no more than 500 miles.
Rameen'south heating bill is $five.42 per month plus $1.08 per therm. How many therms can Rameen use if he wants his heating bill to exist a maximum of $87.l.
- Answer
-
Rameen'southward heating beak is $5.42 per calendar month plus $i.08 per therm. How many therms tin can Rameen employ if he wants his heating nib to exist a maximum of $87.50.
Turn a profit is the money that remains when the costs take been subtracted from the revenue. In the next case, we will observe the number of jobs a small businesswoman needs to do every month in order to make a certain amount of profit.
Felicity has a calligraphy business concern. She charges $two.50 per wedding invitation. Her monthly expenses are $650. How many invitations must she write to earn a turn a profit of at to the lowest degree $2,800 per calendar month?
- Answer
-
\(\begin{array} {ll} {\textbf{Step ane. Read }\text{the problem.}} &{} \\ {\textbf{Footstep 2. Identify }\text{what you are looking for.}} &{\text{the number of invitations Felicity needs to write}} \\ {\textbf{Step 3. Name }\text{what you are looking for.}} &{\text{Let }j=\text{ the number of invitations.}} \\ {} &{} \\ {\infinite\space\infinite\text{Cull a variable to stand for information technology.}} &{} \\ {\textbf{Footstep 4. Translate. }\text{Write a sentence that}} &{} \\ {\text{gives the data to find it.}} &{$two.50 \text{ times the number of invitations}} \\ {} &{\text{minus }$650\text{ is at least }$2,800.} \\ {} &{\infinite\infinite\space two.50j−650\geq 2,800} \\ {\space\space\infinite \text{Translate into an inequality.}} &{} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{\space\space\space\space\space\space\space\infinite\space\space\space\space\space\space\infinite two.5j\geq 3,450} \\ {} &{\space\space\space\infinite\infinite\infinite\space\space\space\space\space\space\space\infinite\space\space\infinite\space\space\space j\geq i,380 \text{ invitations}} \\ {\textbf{Step half dozen. Check }\text{the reply in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {} &{} \\ {} &{} \\ {\infinite\infinite\space \text{If Felicity wrote }1400\text{ invitations, her}} &{} \\ {\infinite\space\infinite \text{profit would be }2.50(1400)−650, \text{or}} &{} \\ {\infinite\space\infinite $2,850.\text{ This is more than }$2800.} &{} \\ {\textbf{Step seven. Write }\text{a judgement that answers the question.}} &{\text{Felicity must write at to the lowest degree }ane,380\text{ invitations.}} \\ \end{array}\)
Caleb has a pet sitting business organisation. He charges $32 per hour. His monthly expenses are $2,272. How many hours must he piece of work in order to earn a profit of at least $800 per month?
- Answer
-
Caleb must work at to the lowest degree 96 hours.
Elliot has a landscape maintenance business organisation. His monthly expenses are $i,100. If he charges $60 per job, how many jobs must he do to earn a profit of at least $4,000 a month?
- Answer
-
Elliot must work at least 85 jobs.
In that location are many situations in which several quantities contribute to the full expense. We must make sure to account for all the individual expenses when we solve issues like this.
Malik is planning a six-twenty-four hour period summertime vacation trip. He has $840 in savings, and he earns $45 per 60 minutes for tutoring. The trip will price him $525 for airfare, $780 for nutrient and sightseeing, and $95 per night for the hotel. How many hours must he tutor to accept enough money to pay for the trip?
- Answer
-
\(\brainstorm{assortment} {ll} {} &{} \\ {\textbf{Footstep 1. Read }\text{the trouble.}} &{} \\ {\textbf{Step ii. Identify }\text{what you are looking for.}} &{\text{the number of hours Malik must tutor}} \\ {\textbf{Step 3. Name }\text{what you are looking for.}} &{} \\ {} &{} \\ {} &{\text{Let }h=\text{ the number of hours.}} \\ {\space\space\space\space\space\space\infinite \text{Cull a variable to represent that}} &{} \\ {\space\infinite\space\space\space\space\space \text{quantity.}} &{} \\ {\textbf{Stride 4. Translate. }\text{Write a judgement that}} &{} \\ {\text{gives the information to find it.}} &{} \\ {} &{\text{The expenses must be less than or equal to}} \\{} &{\text{the income. The price of airfare plus the}} \\{} &{\text{cost of food and sightseeing and the hotel}} \\{} &{\text{bill must exist less than the savings plus the}} \\{} &{\text{amount earned tutoring.}} \\{} &{} \\ {} &{} \\ {} &{} \\ {} &{} \\ {\space\space\infinite\space\space\infinite\space \text{Translate into an inequality.}} &{525+780+95(half-dozen)\leq 840+45h} \\ {\textbf{Stride 5. Solve }\text{the inequality.}} &{} \\ {} &{} \\ {} &{\space\space\space\space\space\space\space\infinite\space\space\infinite\space\space\infinite\space\space 1,875\leq 840+45h} \\ {} &{\infinite\infinite\space\infinite\space\space\space\space\infinite\infinite\space\space\infinite\space\space\space 1,035\leq 45h} \\ {} &{\infinite\space\space\space\space\space\space\space\infinite\space\infinite\space\space\space\space\space\space\space\infinite\space 23\leq h} \\ {} &{\space\space\space\space\space\infinite\space\space\space\infinite\space\space\space\infinite\space\infinite\infinite\space\infinite\infinite\space\space\space h\geq 23} \\ {} &{} \\ {} &{} \\ {\textbf{Step 6. Check }\text{the answer in the trouble}} &{} \\ {\text{and make sure information technology makes sense.}} &{} \\ {\text{We substitute 23 into the inequality.}} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space\space\space\infinite\space\space 1,875\leq 840+45h} &{} \\ {\infinite\infinite\space\space\space\space\space\space i,875\leq 840+45(23)} &{} \\ {\space\space\space\space\infinite\space\space\infinite 1,875\leq 1875} &{} \\ {\textbf{Step 7. Write }\text{a sentence that answers the question.}} &{\text{Malik must tutor at to the lowest degree }23\text{ hours.}} \\ \end{array}\)
Brenda's best friend is having a destination nuptials and the event will terminal 3 days. Brenda has $500 in savings and tin earn $xv an 60 minutes babysitting. She expects to pay $350 airfare, $375 for food and entertainment and $lx a night for her share of a hotel room. How many hours must she babysit to have plenty money to pay for the trip?
- Answer
-
Brenda must babysit at to the lowest degree 27 hours.
Josue wants to go on a 10-night road trip with friends adjacent leap. It will toll him $180 for gas, $450 for nutrient, and $49 per dark to share a motel room. He has $520 in savings and can earn $30 per driveway shoveling snowfall. How many driveways must he shovel to have plenty money to pay for the trip?
- Answer
-
Josue must shovel at least 20 driveways.
Key Concepts
- Inequalities, Number Lines, and Interval Notation
\(x>a \quad x\geq a\quad ten<a\quad x\leq a\)

- Linear Inequality
- A linear inequality is an inequality in one variable that can be written in 1 of the following forms where a, b, and care existent numbers and \(a\neq 0\):
\[ax+b<c, \qquad ax+b\leq c, \qquad ax+b>c, \qquad ax+b\geq c.\nonumber\]
- A linear inequality is an inequality in one variable that can be written in 1 of the following forms where a, b, and care existent numbers and \(a\neq 0\):
- Addition and Subtraction Property of Inequality
- For any numbers a, b, and c, if a<b,thena<b,so
\[\begin{array} {ll} {a+c<b+c} &{a−c<b−c} \\ {a+c>b+c} &{a−c>b−c} \\ \end{array} \nonumber\]
- We tin add together or subtract the same quantity from both sides of an inequality and still keep the inequality.
- For any numbers a, b, and c, if a<b,thena<b,so
- Multiplication and Sectionalization Property of Inequality
- For any numbers a, b, and c,
\(\begin{assortment} {50} \text{multiply or dissever past a }\textbf{positive} \\ \\ \space\space\infinite\space\space\space\space\text{if }a<b\text{ and }c>0,\text{ then } ac<bc\text{ and }\frac{a}{c}<\frac{b}{c}. \\ \infinite\space\space\space\space\space\space\text{if }a>b\text{ and }c>0,\text{ then } ac>bc\text{ and }\frac{a}{c}>\frac{b}{c}. \\ \text{multiply or divide by a }\textbf{negative} \\ \\ \space\space\space\space\space\space\space\text{if }a<b\text{ and }c<0,\text{ then } air-conditioning>bc\text{ and }\frac{a}{c}>\frac{b}{c}. \\ \space\space\infinite\space\space\space\infinite\text{if }a>b\text{ and }c<0,\text{ so } ac<bc\text{ and }\frac{a}{c}<\frac{b}{c}. \\ \terminate{array}\)
- For any numbers a, b, and c,
- Phrases that indicate inequalities
\(>\) \(\geq\) \(<\) \(\leq\) \)" data-valign="middle" grade="lt-math-17389">is greater than is more than
is larger than
exceeds
is greater than or equal to is at least
is no less than
is the minimum
is less than is smaller than
has fewer than
is lower than
is less than or equal to is at most
is no more than
is the maximum
whitworthaltylets.blogspot.com
Source: https://math.libretexts.org/Courses/Las_Positas_College/Foundational_Mathematics/19:_Equations_and_Inequalities/19.01:_Review-_Solve_Linear_Inequalities
0 Response to "Linear Inequalities and Systems of Linear Inequalities Review"
Post a Comment